
万が一の金利上昇に備え、住宅ローン利息の計算方法を覚えよう!
住宅ローンには必ず「利息」がかかります。昨今は超低金利時代と言われていますが、近い将来に金利が上昇するようなことがあれば、いったいどのくらい上がるのでしょうか?今回は、住宅ローンの利息の計算方法について解説します。
01住宅ローンの返済方法
住宅ローンの返済方法には、元利均等返済と元金均等返済があります。仕組みや概要はまったく異なるので、それぞれを詳しく説明します。
元利均等返済
元金と利息を合わせた一定額を毎月支払う返済方法です。毎月の返済額が一定であるため、将来の生活設計が立てやすいのが特徴です。子持ちでこれから教育費などにお金がかかるというような場合には、元利均等返済を選択するのがお勧めです。
一方で、返済開始当初は借入残高が多いので、その分利息が増えます。また、元金均等返済に比べて元金部分の減りが遅くなることから、総返済額が多くなってしまうというデメリットがあります。
元金均等返済
元金が一定で、残高に応じた利息を足した金額を毎月支払う方法です。「元利均等返済」に比べると返済開始当初は毎月の返済額が多くなりますが、元金の減少が早く、また、同じ借り入れ期間の場合、元利均等返済よりも総返済額が安くなるのがメリットです。
元利均等返済と元金均等返済の違い


ただし、総返済額を安く抑えたいからといって、住宅ローンの利用者が毎月の支払額に圧迫されてしまっては意味がありません。毎月の支払額が一定の元利均等返済を選択してから、手元の預金に余裕がある程度できた際に繰り上げ返済をして、支払期間を短縮する方法もあります。どちらの返済方法を選ぶかは、ライフスタイル、収入、将来設計などをよく考慮した上で決めましょう。
また、金融機関の多くは元金均等返済を取り扱っていません。元金均等返済を選択したい場合、取り扱いがあるかどうかを事前に確認してから金融機関を選ぶ必要があります。住宅ローンを利用する上で借入期間、金利、返済金額などと同じように、この返済方法の選択についてもよく検討すべきでしょう。
02元利均等返済で借り入れた場合の返済シミュレーション
元利均等返済と元金均等返済のうち、多くの金融機関が取り扱う元利均等返済によるシミュレーションをします。
元利均等返済(借入額3000万円、返済期間35年)
| 金利 | 毎月返済額 (元金、利息、初回支払い時) |
総返済額 |
| 1% | 8万4685円 元金分:5万9685円 利息分:2万5000円 |
3556万7700円 利息分:556万7700円 |
| 2% | 9万9378円 元金分:4万9378円 利息分:5万円 |
4173万8760円 利息分:1173万8760円 |
| 3% | 11万5455円 元金分:4万455円 利息分:7万5000円 |
4849万1100円 利息分:1849万1100円 |
金利が2%に上がると毎月返済額における利息分が2倍になり、3%になるとさらに増えていく一方で、元金部分が減っています。このようなシミュレーションをすることで、金利上昇による利息負担がどれだけ膨らむのかが、より把握できるでしょう。
毎月返済額や利息、元金などの計算方法
元利均等返済における毎月の返済額は、以下の計算式で算出します。
元利均等返済の毎月の返済額の計算式


利息は毎月の残高に月利を掛けて計算していきます。毎月返済していけば、残高はどんどん減っていきます。そのため、毎回利息は異なってきます。計算をして確認しましょう。
初回支払い時
●利息
初回支払利息の計算式は「初回返済金利(円)=借入残高(円)×金利(%)×1/12」なので、借入額が3000万円、金利が3%の場合で当てはめると、以下のようになります。
3000万円×金利3%×1/12=7万5000円
●元金
毎月の返済額から初回の利息分を引けばいいので、先ほど計算した毎月返済額11万5455円から初回利息分を引きます。
11万5455円−7万5000円=4万455円
●残高
借入金額から初回に返済した元金を引きます。ここで利息分まで引かないように注意が必要です。
3000万円−4万455円=2995万9545円
次に2回目の支払いについて計算していきましょう。計算方法は初回と同様です。
2回目支払い時
●利息
初回返済後の残高は2995万9545円なので、以下のようになります。
2995万9545円×金利3%×1/12=7万4898円(端数は切り捨て)
●元金
元利均等返済は毎月の返済額が変わりません。毎月返済額の11万5455円から今回の利息分を引いて計算をします。
11万5455円−7万4898円=4万557円
●残高
1回目の返済後の借入残高2995万9545円から今回の元金を引きます。
2995万9545円-4万557円=2991万8988円
最後に3回目に支払いについて計算します。
3回目支払い時
●利息
2回目返済後の残高は2991万8988円なので、以下のようになります。
2991万8988円×金利3%×1/12=7万4797円(端数は切り捨て)
●元金
初回、2回目と同じように、毎月返済額の11万5455円から今回の利息分を引いて計算をします。
11万5455円−7万4797円=4万658円
●残高
2回目の返済後の借入残高2991万8988円から今回の元金を引きます。
2991万8988円-4万658円=2987万8330円
初回から3回目までのシミュレーションを見てみると、元金があまり減っていかないのが分かります。また、毎月の支払額は一定ですが、元金が少しずつ増えていき、利息がわずかに減っています。今回は金利を3%で計算していますが、もしも金利が上昇したら、利息分の負担は当然増えます。最初に借り入れした条件でそのまま何も検討せず返済していくのではなく、今回のような計算式を用いて、どのように支払っていくのか、どこかで繰り上げ返済ができないかなど、数年に1度は検討し直すことも大切でしょう。
※あくまでシミュレーションによる試算であり、実際の金額とは異なる場合があります。
03Excelを使った利息計算の方法
Excelには「元利均等返済」を求める関数式が含まれています。Excelの財務関数を使い、月々の返済額のうちの利息分を求めるには、「IPMT関数」を利用します。数式は以下のようになります。
Excelを使った利息計算の数式
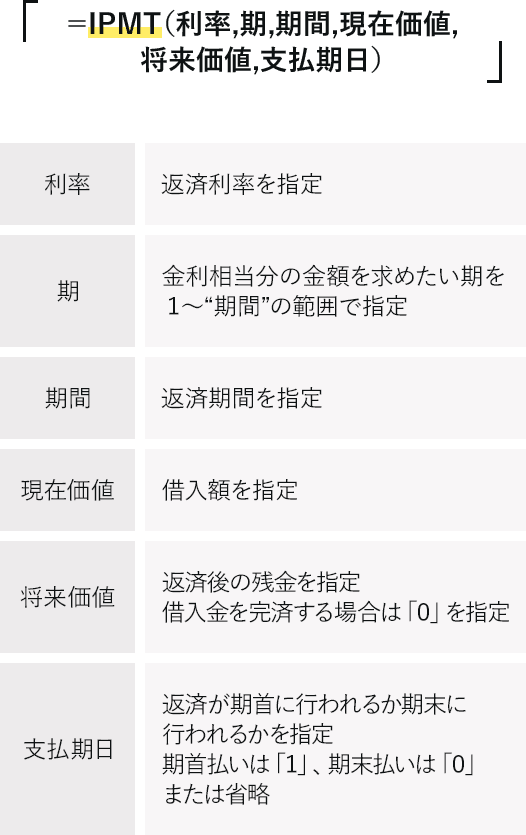

上記の関数を用いて、借入金額 3000万円、年利1%、返済期間35年で住宅ローンを組み、返済方法は元利均等返済方式として1回目に支払う利息額を求めます。ポイントは「利率」「期」「期間」の単位を同じにすること。「利率」は年利を12で割り、月利で指定します。「期間」は借入期間に12を掛けて月回数にします(今回の場合は35×12)。
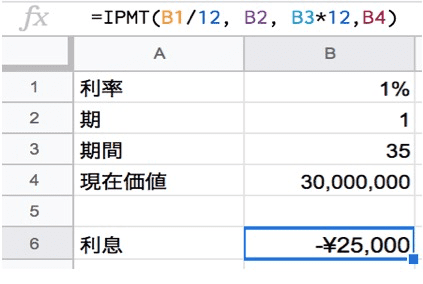
下記の画像のように、支払いの場合の計算結果はマイナスで表示され、手元に残る金額はプラスで表示されます。今回の場合、1回目に支払う利息は2万5000円になります。
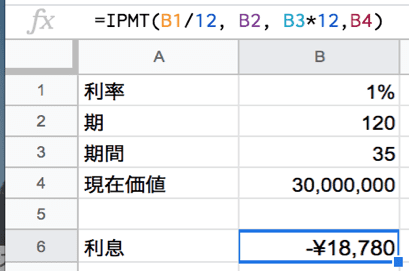
仮に10年目末の支払いについて計算してみると、120回目の支払い利息額は1万8780円になります。
このようにExcelの財務関数を使えば、簡単に利息分の計算ができます。自分でシミュレーションができれば、金利プランや返済期間などを検討する際のヒントにもなり、どれだけ利息分を支払っているのかも明確になります。

文・監修:下澤一人
宅地建物取引士
プロフィール
出版社勤務後、宅地建物取引士の資格を取得し、不動産専門新聞記者、不動産会社勤務を経て現在、編集者・ライターとして活動中。
関連キーワード
















